prisoners' dilemma

The classic problem in game theory . Two prisoners jointly charged with a crime are held apart, and each is given the option of confessing, or not confessing. If neither confesses, the prosecutor will find a lesser charge, and each will serve two years. If each confesses, he convicts them both, and they will serve six years each. If A confesses and B does not, A is released and B serves an aggravated ten years. If B confesses and A does not, B is released, and A serves an aggravated ten years. The matrix is shown in the figure:

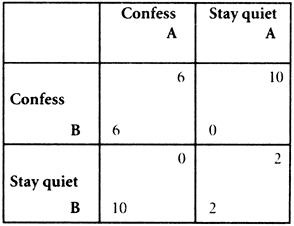The surprising truth about the game is that whatever the other prisoner does a prisoner does better by confessing (if A confesses, B does better for himself by confessing, and if A does not confess, B does better for himself by confessing; and conversely for A if B confesses or does not confess). Confessing dominates not confessing. Yet the social result in which each of A and B follows this reasoning is the worst of all (12 person-prison years) and together they would have done much better by sitting tight (4 person-prison years). Many political situations (e.g. whether to vote when there is a cost to doing so, whether to refrain from wage-bargaining, whether to be a good citizen and turn off one's hose during a water shortage) can be modelled as prisoners' dilemmas. The structure shows that it is not always the case that the social good is furthered efficiently by each person doing what is in his or her own best interests: as well as an ‘invisible hand’ whereby unbridled self-interest elevates everybody's position, there can be an invisible boot whereby it diminishes it (see Smith, Adam).

An iterated prisoners' dilemma is a sequence of such situations, of either finite or infinite length. In an interesting study (The Evolution of Cooperation, 1984) Robert Axelrod showed that an efficient policy in such a situation is ‘tit for tat’: you start off co-operating (not confessing) until faced with a play on which the opponent ‘rats’, and then you rat (confess) once in retaliation, but then, if the opponent mends his ways, you go back to not confessing until the same thing happens again. As well as being an efficient strategy ‘tit for tat’ has some intuitive moral justification. However, the strategy is sensitive to the ratio of rewards and penalties that are in play, and cannot be said to be the single best strategy for all circumstances.