diagonal procedure

The method first used by Cantor to show that there cannot be an enumeration of the real numbers. Any real number can be written as an infinite decimal. So we imagine a correspondence with the natural numbers, giving us some real as the first, another as the second, and so on. Given such a list, Cantor defines a real number that differs from the first real in the first decimal place, the second in the second place, and so on for every listed real. Thus if the decimal expansion of the first real is written as the sequence of digits x 01 x 02 x 03… and the reals are laid out in order:

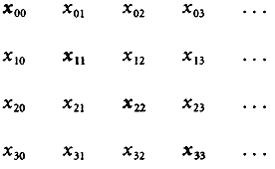We then consider the diagonal (highlighted) real x ₀₀ x ₁₁ x ₂₂…and define a non-terminating decimal that differs in each place: e.g. let y _nn = 5 if x _nn ? 5, and y _nn = 6 otherwise. This then is a real that was not on the original list, for it differs from the nth real on the list in the nth place. The construction refutes the thesis that we had enumerated all the reals. Diagonal arguments are one of the most powerful tools of set theory and metamathematics . They also bear a close relationship to arguments of the Liar family: an explicit use of diagonal reasoning occurs in Richard's paradox.